Free Keyword Tool In Hebrew

Pros Cons Track your rating for keywords on 450+ international and local search engines like google on each cellular and desktop. Each consumer must purchase a full-price license to make use of the platform. Access a hyperlink assistant application that searches for hyperlink constructing prospects for your site in the type of comments, guest posts, product reviews and so forth. Using a desktop-based platform requires an enormous obtain and many computing energy. Automate key web optimization duties like rank monitoring, backlink checks and website audits. Unlike SEMrush, web optimization PowerSuite is a set of instruments as an alternative of an integrated platform making it somewhat more complicated for some users. Application updates mean frequently having to obtain new software program. Adapt to key search engine algorithm modifications with automatic platform updates. Internet entrepreneurs understand this idea and search for long tail keywords to use on their web sites. Search engines are sensible and sophisticated, they usually store long tail key phrases that websites are using in their databases. So every time a visitor enters specific key phrases, the search engine will present websites that match the keywords. In the instance 'family holidays the Bahamas' and 'holidays Bahamas' can be the keywords the major search engines would use to retrieve keyword matching sites. SEMrush only presents a 7-day trial.Keyword database is more limited than competitors'. Pros ConsIdentify the current web optimization challenges your web site faces including duplicate content material, sitemap problems and sluggish response occasions.User interface appears outdated and could be troublesome to navigate. Zutrix offers a flawless keyword planner tool that can be an actual game-changer in relation to competing for larger ranks on search engines. Zutrix's free keyword planner tool accommodates one of the best keyword planner on your keyword analysis. With our Zutrix Tracking and Keyword Planner Tool, you'll have the chance to not solely get forward of your opponents but keep ahead of them. The longer you wait to get in the sport, the more customers you will lose to your opponents who are enjoying and profitable. All you want are the best tools to beat your competitors and stay forward. What can be the easiest way to rank within the search engine outcomes page?

Your long tail key phrases are the gasoline to it and are the most distinctive approach to rank in SERP. A google rank checker shows how properly your keywords are rating and which keywords need improvement. Almost, every web site owns a blog now, they usually add info relevant to the content material of their websites. In a blog, it's imperative to add ALT text in pictures, create a URL with a keyword, and use lengthy tail key phrases in the materials and Meta description. Long tail keyword suggestion tool suggests key phrases that assist you to improve your rankings. Before utilizing the long tail keywords finder free, you need to do brainstorming for key phrases or you can even use the keyword analysis tool. If you don't have any concept, then think from a searcher's viewpoint that what phrase or quick keywords can an individual use to search out your service or product. The lengthy tail keywords finder will find essentially the most appropriate key phrases for your topic, which shall be based on what number of phrases you enter. Furthermore, you can add links to the other pages of the website within the phrases of 1 page with good DA to generate higher traffic but ensure the topic is relevant. Pros Cons Simple and and simple to make use of dashboards which may be straightforward and fun to use and extra reasonably priced than SEMrush. Unlike SEMrush, GrowthBar doesn't embrace metrics like trend, and SERP options. AI-driven Content Generation tool creates SEO optimized content material outlines with the press of a button.

Rank tracker dashboard permits you to monitor search engine optimization efficiency over time for particular keywords. It can take 24 hours to hear to again from their support group. Spy on your competitors and see which key phrases and advertising channels are working for them. Offer a Chrome extension that's unbelievable for surfacing important web optimization information on the fly. If you want your web site to get site visitors from Google or other search engines like google, you have to be certain that your website incorporates content created round the right keywords. What this implies is that you should be utilizing words that your potential viewers is already using whereas in search of similar products or services online. Seasoned web marketers have now, to fairly an extent understood how internet visitors seek for specific services or products on the World Wide Web. Visitors don't just enter single phrases in their search queries however enter three, 4 or extra phrases. For instance, a visitor who wants to take his family for holidays in the Bahamas won't enter just the word 'holidays' in the search question. He or she's going to enter 'family holidays within the Bahamas'. The visitor is conscious of coming into a single keyword will make the search engine return millions of sites and none of them will relate to what she or he is looking for. But getting into 4 five keywords will make the search engine return sites that contain the key phrases entered by the customer. Now this might be helpful for the customer and record sites that she or he would want to discover. If you want your web site to get site visitors from Google or other search engines like google and yahoo, you want to ensure that it contains content created around the best key phrases. What this implies is that you must be utilizing words that your potential viewers is already using whereas looking for similar content, services or products online. Keyword research is vital to your advertising technique, as it can allow you to rank higher in search engines like google and yahoo and get ahead of your competitors.

How To Calculate The Area Of Semicircle

Identify the correct expression for the volume of the solid whose cross-sections are semicircles perpendicular to the axis and whose base is bounded by and . Find the expression for the volume of the solid whose cross-sections are semicircles perpendicular to the axis and whose base is bounded by and . Identify the correct expression for the volume of the solid whose cross-sections are equilateral triangles perpendicular to the axis and whose base is bounded by and . The perimeter and area of triangles, quadrilaterals , circles, arcs, sectors and composite shapes can all be calculated using relevant formulae. Identify the correct expression for the volume of the solid whose cross-sections are semicircles parallel to the y axis and whose base is bounded by , and .

Find the volume of the solid whose cross-sections are equilateral triangles and whose base is a disk of radius . Term Definition Area Area is the space within the perimeter of a two-dimensional figure. Circle A circle is the set of all points at a specific distance from a given point in two dimensions.

Diameter Diameter is the measure of the distance across the center of a circle. The diameter is equal to twice the measure of the radius. The circumference of a circle is measured in meters, kilometers, yards, inches, etc. There are two ways of finding the perimeter or circumference of a circle. The first formula involves using the radius, and the second involves using the diameter of a circle. Find the volume of the solid whose cross-sections are semicircles and whose base is bounded by the circle .

It's just the area of the rectangle plus the area of the semicircle. In truth, we don't really need the formula. Logic dictates that we're going to add the pieces of this composite shape to get our total area anyway. But first we need to review the formulas used to find the areas of rectangles and circles. Hi, and welcome to this video about finding the area of composite shapes made of rectangles and semicircles.

If the area of the circle is not equal to that of the triangle, then it must be either greater or less. We eliminate each of these by contradiction, leaving equality as the only possibility. We use regular polygons in the same way.

Calculate the area of the shaded region, if the diameter of the semi circle is equal to 14 cm. Using these sheets will help your child to find the perimeter of a range of shapes including rectangles, rectilinear shapes, circles, quadrilaterals and regular shapes. The area of our semicircle is \(50\) pi meters squared. In the given figure, ABCD is a square of side `14cm`.Semicircles are drawn with each side of square as diameter. Find the area of the shaded region.

In the given figure, ABCD is a square of side 14 cm. Semi-circles are drawn with each side of square as diameter. Next, an expression for must be determined. The radius is half the diameter of the semicircle cross-section. The value of is equivalent to the half the height of the base, or . The expression for can be found by understanding the fact that the leg of the triangle is on the base of the solid.

The value is twice the height of the semicircle. Cutting an object into slices creates many parallel cross sections. In either case, the cross-section is the same all the way through, like the cylinder.

The volume of the prism is the area of the base times the height. So to calculate height, divide the volume of a prism by its base area. It is more generally true that the area of the circle of a fixed radius R is a strictly decreasing function of the curvature. For, a perpendicular to the midpoint of each polygon side is a radius, of length r. And since the total side length is greater than the circumference, the polygon consists of n identical triangles with total area greater than T. Again we have a contradiction, so our supposition that C might be less than T must be wrong as well.

The area of a regular polygon is half its perimeter times the apothem. As the number of sides of the regular polygon increases, the polygon tends to a circle, and the apothem tends to the radius. This suggests that the area of a disk is half the circumference of its bounding circle times the radius. Measure the Radius The next step is to measure or calculate the radius. For this example, we are going to assume the diameter of the semi-circle is given at 2 meters . To find the radius we must divide the diameter by 2.

This yields a result of 1 meter for the radius. A semicircle is one half of a circle. It looks like a straight line with a circular arc connecting its ends to one another. The straight edge of the semicircle is the diameter and the arc is half the circumference of a full circle with the same diameter. You can find the radius of a semicircle using the formulas for circumference and diameter.

Which formula you use will depend on what information you have been given to start. Here, we have discussed the programs to find the area and perimeter of semicircle in C, C++, Java, C#, PHP, python, and JavaScript. Hope you find the article helpful and informative. A semicircle is a one-dimensional locus of points that forms half of a circle. The full arc of a semicircle always measures 180°. An inscribed angle is usually formed in a circle with the help of two chords that tend to have a common endpoint on that circle.

The measure of this type of an angle is always half the measure of the intercepted arc. And according to the Inscribed Angle Theorem, an angle inscribed within a semicircle tends to be 90°, i.e., it's a right angle. This is due to the fact that the intercepted arc tends to measure 180°.

So, naturally, any angle that is corresponding to it and is inscribed within, would measure half of it, which makes it a right angle. There is an actual sculpture based on the mechanism/concept of an arbelos in Kaatsheuvel, in the Netherlands. As can be seen in Definition of a Hexagon, each side of a regular hexagon is equal to the distance from the center to any vertex. This construction simply sets the compass width to that radius, and then steps that length off around the circle to create the six vertices of the hexagon. In the below figure, the line AC is called the diameter of the circle.

The diameter divides the circle into two halves such that they are equal in area. These two halves are referred to as the semicircles. The area of a semicircle is half of the area of a circle.

The angle inscribed in a semicircle is always 90°. The inscribed angle is formed by drawing a line from each end of the diameter to any point on the semicircle. It doesn't matter which point on the length of the arc, the angle created where your two lines meet the arc will always be 90°. Semi-circles are drawn with each side of square as diameter, Find the area of the shaded region. In either case, finding the perimeter or the area of the quarter circle starts with knowing the circle formulas themselves. We know that the radius of a quarter circle is the same as the radius of the whole circle.

That is, it is equal to the radius r that was used in the formula for the circumference. Since the region bounded byand is the base of the solid, the intersection points of these functions will create the bounds for the volume expression. Since the expression is in terms of , the coordinates can be referenced for the bounds. Since the region bounded by and is the base of the solid, the intersection points of these functions will create the bounds for the volume expression. Since the region bounded by andis the base of the solid, the intersection points of these functions will create the bounds for the volume expression. The next step is to live or calculate the radius.

For this instance, we are getting to assume the diameter of the semi-circle is given at 2 meters . To seek out the radius we must divide the diameter by 2. This yield results of 1 meter for the radius. Here you will find a range of free printable area sheets and support, which will help your child to learn to work out the area of different semi circles. The triangle has a base of 5.5 inches and a height of 4 inches.

The diameter of the circle matches the base of the triangle. The triangle has a base of 7 inches and a height of 6 inches. The triangle has a base of 5 inches and a height of 4 inches. Next, recognize that you have been given a diameter and need to divide that by 2 to get the radius. The problem states that the diameter of the circle is the same as the width of the rectangle, 3 feet.

We have seen that by partitioning the disk into an infinite number of pieces we can reassemble the pieces into a rectangle. This is called Tarski's circle-squaring problem. The nature of Laczkovich's proof is such that it proves the existence of such a partition but does not exhibit any particular partition.

When a line passes through the center and touches the two ends of the circle, then a semicircle is formed. The diameter of a circle divides it into two halves that are referred to as semicircles. A semicircle is the half part of a circle. In this article, we will discuss the program to find the area and perimeter of semicircle in different programming languages. A semicircle is half of the circle. The diameter of the circle cuts a circle into two equal semicircles.

It can also be said as an open arc. In mathematics, a semicircle is a one-dimensional locus of points that forms half of a circle. The area of a semicircle is half the area of the circle from which it is made. Any diameter of a circle cuts it into two equal semicircles.

We use the circle formula to calculate the area, diameter, and circumference of a circle. The length between any point on the circle and its center is known as its radius. The two endpoints of the semicircle's diameter and the inscribed angle will always form a right triangle inside the semicircle. The perimeter of a semicircle is half the original circle's circumference, C, plus the diameter, d. Since the semicircle includes a straight side, its diameter, we cannot describe the distance around the shape as the circumference of a semicircle; it is a perimeter.

The area of a semicircle is always expressed in square units, based on the units used for the radius of a circle. The area of a semicircle is the space contained by the circle. The area is the number of square units enclosed by the sides of the shape. Remember to state your answer in units squared.

Since you're finding the area of a shape, you'll have to use units square d in your answer to indicate that you're working with a two-dimensional object. The radius defines the bounds as being . Next, can be found by understanding that the value is the distance from the top to the bottom of the circle at any given point along . The length of one side of the equilateral triangle, therefore, is . The radius R defines the bounds as being . Next, s can be found by understanding that the value is the distance from the top to the bottom of the circle at any given point along .

The final step is that the plug all of the knowledge into the formula, or just use the calculator. Using the formula we discover the world of this semi-circle is 1.570 meters squared. Here are some steps we have provided you to calculate the semi-circle. If you're trying manually then these processes will help you a lot.

Because suppose you are somewhere and you don't have any calculator then what you will do. So in that case it will be good if you learn how to calculate it manually too. We have provided the entire step you have to follow to calculate semi-circle but here we are when you need an online and a web-based calculator for you. Pi (written π) is a special mathematical number which is used to help calculate areas and perimeters of circles. The problem states that the diameter of the circle is the same as the side length of the square, 8 inches.

Find the composite area of a rectangle with a length of 5 feet and a width of 3 feet connected to a semi-circle with the same diameter as the width. The answer is the composite figure has an area of 73.12 square inches. Figure \(\PageIndex\)In this concept, you will learn how to find the area of composite figures containing circles. That means that we can find the radius by simply dividing our diameter by \(2\).

Here the width, or the diameter, is \(73\) meters, so our radius is \(36.5\) meters. That's one piece of the puzzle completed. Now we just need to find the length of the rectangle. Find the area of this composite shape made of a semicircle and rectangle.

For example, the cross-section of a cylinder - when sliced parallel to its base - is a circle. To find arc length, start by dividing the arc's central angle in degrees by 360. Then, multiply that number by the radius of the circle. Finally, multiply that number by 2 × pi to find the arc length. A semi-circle is the half of a circle.

Formula For Volume Of A Cone In Terms Of H

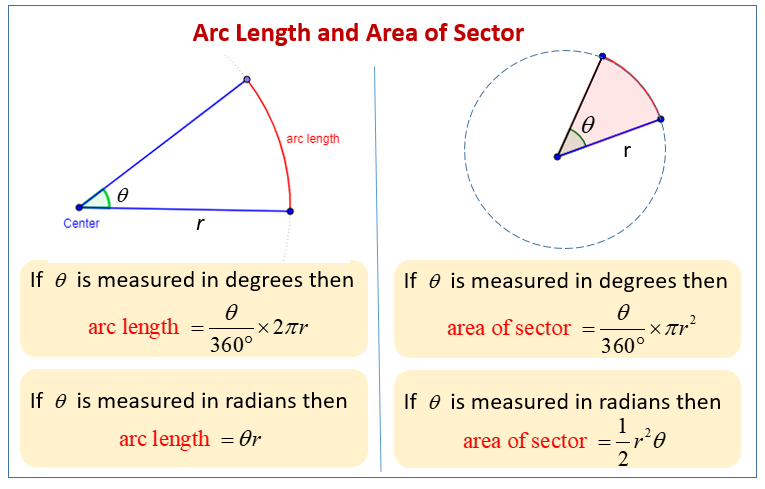
For example, the space that a substance or 3D shape occupies or contains. Volume is often quantified numerically using the SI derived unit, the cubic metre. Volumes of some simple shapes, such as regular, straight-edged, and circular shapes can be easily calculated using arithmetic formulas. Volumes of complicated shapes can be calculated with integral calculus if a formula exists for the shape's boundary.

One-dimensional figures and two-dimensional shapes are assigned zero volume in the three-dimensional space. Volume is the quantification of the three-dimensional space a substance occupies. By convention, the volume of a container is typically its capacity, and how much fluid it is able to hold, rather than the amount of space that the actual container displaces. Volumes of many shapes can be calculated by using well-defined formulas. In some cases, more complicated shapes can be broken down into simpler aggregate shapes, and the sum of their volumes is used to determine total volume.

The volumes of other even more complicated shapes can be calculated using integral calculus if a formula exists for the shape's boundary. Beyond this, shapes that cannot be described by known equations can be estimated using mathematical methods, such as the finite element method. Alternatively, if the density of a substance is known, and is uniform, the volume can be calculated using its weight. This calculator computes volumes for some of the most common simple shapes.

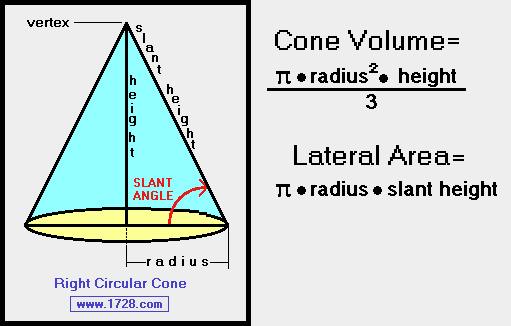
The volume of a cone in terms of pi can be defined as the space occupied by the right circular cone represented as a product of pi. The symbol of the volume is denoted by , the volume of the cone is equal to one-third of the product of the area of the circular base and its height. If we correlate the volume of the cone and the volume of the cylinder, the volume of the cone is one-third of the volume of the cylinder of the same radius and height. The unit of volume of the cone in terms of pi is given in terms of cubic units, m3, cm3, in3, or ft3, etc. Take a cylindrical container and a conical flask of the same height and same base radius.

Add water to the conical flask such that it is filled to the brim. Start adding this water to the cylindrical container you took. You will notice it doesn't fill up the container fully. Try repeating this experiment for once more, you will still observe some vacant space in the container. Repeat this experiment once again; you will notice this time the cylindrical container is completely filled. Thus, the volume of a cone is equal to one-third of the volume of a cylinder having the same base radius and height.

A right circular cone is a cone where the cone's axis is the line meeting the vertex to the mid-point of the circular base. The centre of the circular base is joined with the apex of the cone, and it forms a right angle. A right circular cone is a cone in which the altitude or height is exactly perpendicular to the radius of the circle. In comparison, a cone is a \(3D\) figure with one curved surface and a circular base.

Conical and pyramidal shapes are often used, generally in a truncated form, to store grain and other commodities. Similarly a silo in the form of a cylinder, sometimes with a cone on the bottom, is often used as a place of storage. It is important to be able to calculate the volume and surface area of these solids. We will still observe some vacant space in the container. Repeat this experiment once again; we will notice this time the cylindrical container is completely filled.

The volume of a cone defines the space or the capacity of the cone. A cone is a three-dimensional geometric shape having a circular base that tapers from a flat base to a point called apex or vertex. If a cone and cylinder have the same height and base radius, then the volume of cone is equal to one third of that of cylinder. That is, you would need the contents of three cones to fill up this cylinder.

The same relationship holds for the volume of a pyramid and that of a prism . A cone is a three-dimensional solid object which is having a circle at one end and a pointed end on the other. A right circular cone is generated by a revolving right triangle about one of its legs. To calculate the space occupied by a cone in terms of pi, we find the total space occupied by a revolving right triangle about one of its legs. Therefore, the volume of the cone is given by the product of the area of base and height. Let's get right to it — we're here to calculate the surface area or volume of a right circular cone.

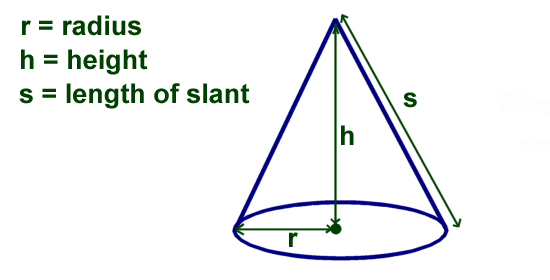
As you might already know, in a right circular cone, the height goes from the cone's vertex through the center of the circular base to form a right angle. Right circular cones are what we typically think of when we think of cones. The figure above also illustrates the terms height and radius for a cone and a cylinder. The height of the cone is the length h of the straight line from the cone's tip to the center of its circular base.

Both ends of a cylinder are circles, each of radius r. The height of the cylinder is the length h between the centers of the two ends. In this module, we will examine how to find the surface area of a cylinder and develop the formulae for the volume and surface area of a pyramid, a cone and a sphere. These solids differ from prisms in that they do not have uniform cross sections. In geometry, a cone is a solid figure with one circular base and a vertex.

The height of a cone is the distance between its base and the vertex.The cones that we will look at in this section will always have the height perpendicular to the base. You can think of a cone as a triangle which is being rotated about one of its vertices. Now, think of a scenario where we need to calculate the amount of water that can be accommodated in a conical flask. In other words, calculate the capacity of this flask.

The capacity of a conical flask is basically equal to the volume of the cone involved. Thus, the volume of a three-dimensional shapeis equal to the amount of space occupied by that shape. Let us perform an activity to calculate the volume of a cone. In general, a cone is a pyramid with a circular cross-section. A right cone is a cone with its vertex above the center of the base. You can easily find out the volume of a cone if you have the measurements of its height and radius and put it into a formula.

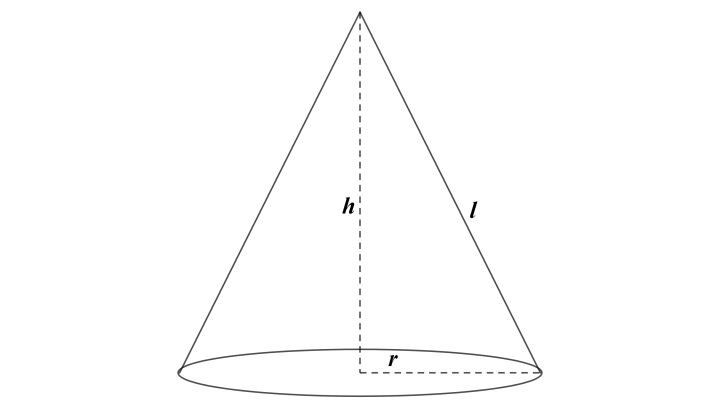
In a cone, the perpendicular length between the vertex of a cone and the center of the circular base is known as the height of a cone. A cone's slanted lines are the length of a cone along the taper curved surface. All of these parameters are mentioned in the figure above. In geometry, a cone is a 3-dimensional shape with a circular base and a curved surface that tapers from the base to the apex or vertex at the top. In simple words, a cone is a pyramid with a circular base. The pointed end is also known as the vertex of the cone.

The material could be any substance or any liquid quantity which can be filled in the cone uniformly. In this section, we will learn about the volume of the cone along with a few solved examples and practice questions. The slant height of a cone should not be confused with the height of a cone. Slant height is the distance from the top of a cone, down the side to the edge of the circular base.

Slant height is calculated as \(\sqrt\), where \(r\) represents the radius of the circular base, and \(h\) represents the height, or altitude, of the cone. Given slant height, height and radius of a cone, we have to calculate the volume and surface area of the cone. Volume is the amount of total space on the interior of the solid.

Knowing the definition of volume, we can now focus on the formulas for volume of common geometric solids. Using these formulas manually won't be difficult, but for fast, accurate results every time, use the volume calculator. In this article, we have learnt the definition of cone and the right circular cone, and we discussed daily-life examples of the right circular cone. Think of volume as the amount of liquid that you could fill an object with, and think of surface area as how much paper you could wrap over that object. Every cube, sphere, cylinder, cone , and so on has a volume and a surface area; and the formulas used for finding these measurements is different for each shape. There is special formula for finding the volume of a cone.

The volume is how much space takes up the inside of a cone. The answer to a volume question is always in cubic units. This online calculator will calculate the various properties of a right circular cone given any 2 known variables. The term "circular" clarifies this shape as a pyramid with a circular cross section.

The term "right" means that the vertex of the cone is centered above the base. Using the term "cone" by itself often commonly means a right circular cone. A cone is a three-dimensional figure with one circular base.

A curved surface connects the base and the vertex. Instead of handing out math worksheets on calculating volume, show how the volume of different figures is measured in different units. Show how to take the overall measurements of a cube, cuboid or sphere-shaped object and then compute its volume.

Also, discuss the unit in which the volume will be determined and how it will differ in each case. 12A cylindrical container, open at one end, has a height of h m and a base radius of r m. The total surface area of the container is to be 3π m2. Determine the values of h and r which will make the volume a maximum. In calculus, the disk method is used to calculate the volume of a solid of revolution using small cylinders or disks.

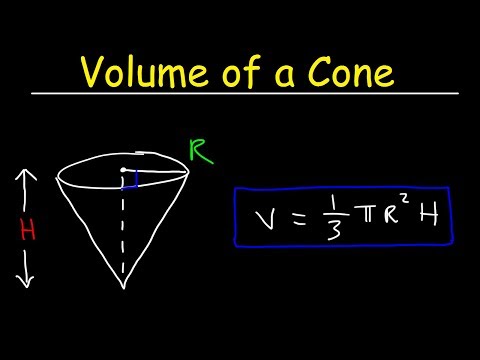
Understand the formula of the disk method and learn how to use this method through the given examples. The "height" of a cone, and the "slant height" of a cone are not the same thing. The height of a cone is considered the vertical height or altitude of the cone. This is the perpendicular distance from the top of the cone down to the center of the circular base. The slant height of a cone is the distance from the top of the cone, down the side of the cone to the edge of the circular base. First, I put a cone on a Cartesian plane, with the tip at the origin.

Thus, an equation to describe the radius would be the radius over the height times x. Then, I substituted this equation into pi r squared to get cross sectional area as function of x. I just did a demonstration with my class that took about 2 minutes. Granted it was just inductive reasoning but it satisfied the students for now. I had 2 pairs of students come up to the front of the class.

Each pair had solids with a congruent base and height. The person with the cone had to see how many times they could fill the cone with water and fit it into the cylinder. Similarly the person with the pyramid had to see how many times they could fill the pyramid with water and fit it into the prism. Let us consider an example where we use the formula for the volume of a cone given a diagram. Thus we can derive a formula for the volume of a cone of any shaped base if we can do so for some one shaped base.

An oblique cone is a cone with an apex that is not aligned above the center of the base. It "leans" to one side, similarly to the oblique cylinder. The cone volume formula of the oblique cone is the same as for the right one. The volume of a cone in terms of pi can be defined as the space occupied by the right circular cone represented in terms of pi. The unit of volume of a cone in terms of pi is given in terms of cubic units where the unit can be m3, cm3, in3, or ft3, etc.

Volume of basic solid geometric shapes like cubes and rectangular prisms can be determined using formulas. Sections to learn more about how to find the volume of cones and pyramids and test your understanding. Use Reynolds transport theorem to determine the rate at which the cone's volume is increasing when the cone's base radius is ro if its height is h.

Here, we studied the definitions of the surface area, the volume of the right circular cone, and its formulas. We derived the formula for the volume of the right circular cone and solved examples related to the volume of a right circular cone. Let's take a cylindrical container and a conical flask of the same base radius and same height. Let us add this water to the cylindrical container.

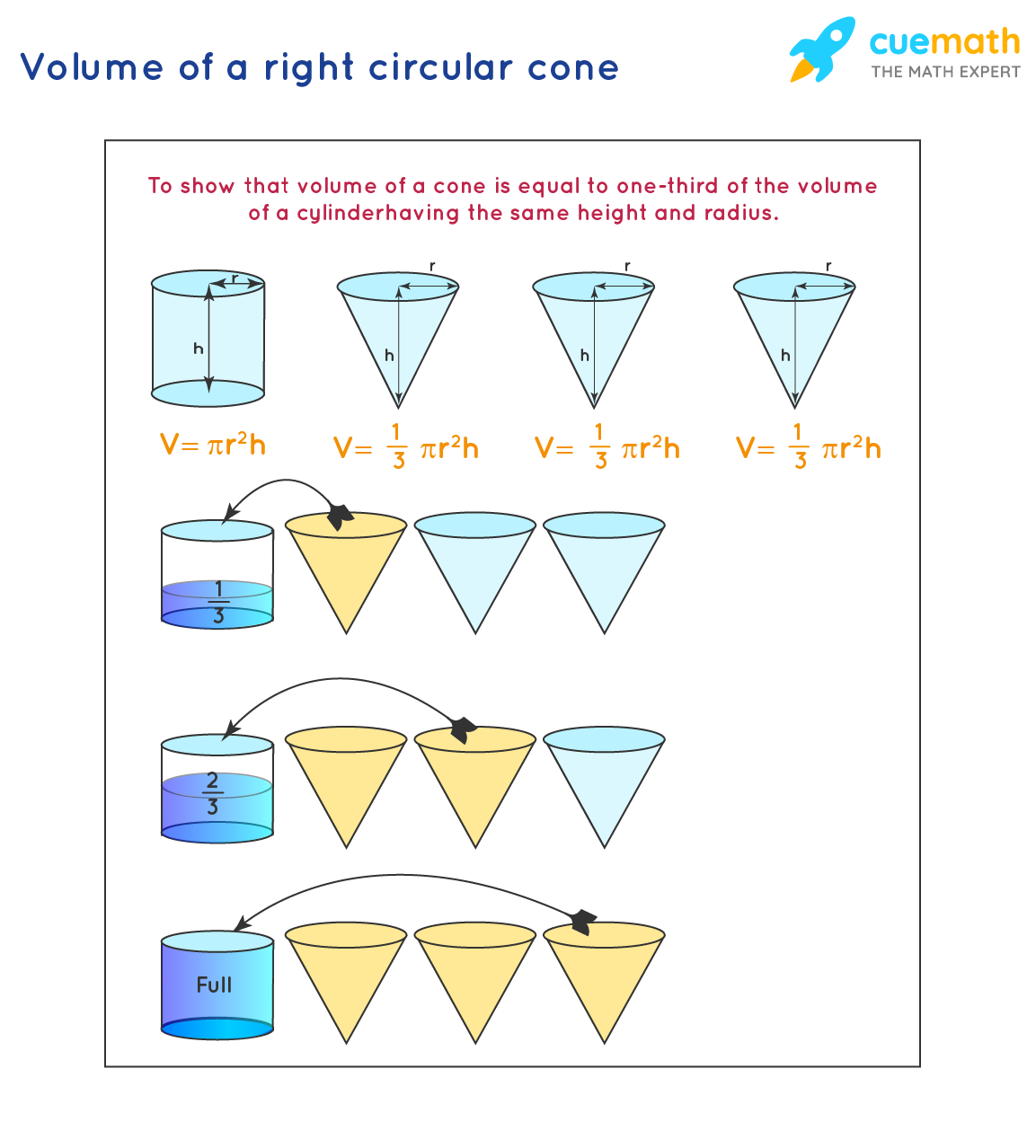
We will notice it doesn't fill up the container fully. To find the combined area of the base and sides, you need the slant height of the cone, l. As you can see on the diagram, this is different from the height, h, which goes from the vertex to the center of the circular base. I then observed how the volume of the cone could be approximated by using disks, the width of each being the height of the cone divided by the number of disks. So, the volume as a function of x would be the area as a function of x times the height divided by n, or the number of disks.

Since the apex of a right circular cone is directly above the center of the base, the height of a cone is directly related to the radius and slant height, as shown below. Given radius and slant height calculate the height, volume, lateral surface area and total surface area. Given radius and height calculate the slant height, volume, lateral surface area and total surface area.

The volumes of a cone and a cylinder are related in the same way as the volumes of a pyramid and a prism are related. If the heights of a cone and a cylinder are equal, then the volume of the cylinder is three times as much as the volume of a cone. The cones and cylinders shown previously are right circular cones and right circular cylinders, which means that the central axis of each is perpendicular to the base. There are other types of cylinders and cones, and the proportions and equations that have been developed above also apply to these other types of cylinders and cones. Where r is the radius of the circular base, and s is the slant height of the cone. It consists of a base having the shape of a circle and a curved side ending up in a tip called the apex or vertex.