How To Calculate The Area Of Semicircle

Identify the correct expression for the volume of the solid whose cross-sections are semicircles perpendicular to the axis and whose base is bounded by and . Find the expression for the volume of the solid whose cross-sections are semicircles perpendicular to the axis and whose base is bounded by and . Identify the correct expression for the volume of the solid whose cross-sections are equilateral triangles perpendicular to the axis and whose base is bounded by and . The perimeter and area of triangles, quadrilaterals , circles, arcs, sectors and composite shapes can all be calculated using relevant formulae. Identify the correct expression for the volume of the solid whose cross-sections are semicircles parallel to the y axis and whose base is bounded by , and .

Find the volume of the solid whose cross-sections are equilateral triangles and whose base is a disk of radius . Term Definition Area Area is the space within the perimeter of a two-dimensional figure. Circle A circle is the set of all points at a specific distance from a given point in two dimensions.

Diameter Diameter is the measure of the distance across the center of a circle. The diameter is equal to twice the measure of the radius. The circumference of a circle is measured in meters, kilometers, yards, inches, etc. There are two ways of finding the perimeter or circumference of a circle. The first formula involves using the radius, and the second involves using the diameter of a circle. Find the volume of the solid whose cross-sections are semicircles and whose base is bounded by the circle .

It's just the area of the rectangle plus the area of the semicircle. In truth, we don't really need the formula. Logic dictates that we're going to add the pieces of this composite shape to get our total area anyway. But first we need to review the formulas used to find the areas of rectangles and circles. Hi, and welcome to this video about finding the area of composite shapes made of rectangles and semicircles.

If the area of the circle is not equal to that of the triangle, then it must be either greater or less. We eliminate each of these by contradiction, leaving equality as the only possibility. We use regular polygons in the same way.

Calculate the area of the shaded region, if the diameter of the semi circle is equal to 14 cm. Using these sheets will help your child to find the perimeter of a range of shapes including rectangles, rectilinear shapes, circles, quadrilaterals and regular shapes. The area of our semicircle is \(50\) pi meters squared. In the given figure, ABCD is a square of side `14cm`.Semicircles are drawn with each side of square as diameter. Find the area of the shaded region.

In the given figure, ABCD is a square of side 14 cm. Semi-circles are drawn with each side of square as diameter. Next, an expression for must be determined. The radius is half the diameter of the semicircle cross-section. The value of is equivalent to the half the height of the base, or . The expression for can be found by understanding the fact that the leg of the triangle is on the base of the solid.

The value is twice the height of the semicircle. Cutting an object into slices creates many parallel cross sections. In either case, the cross-section is the same all the way through, like the cylinder.

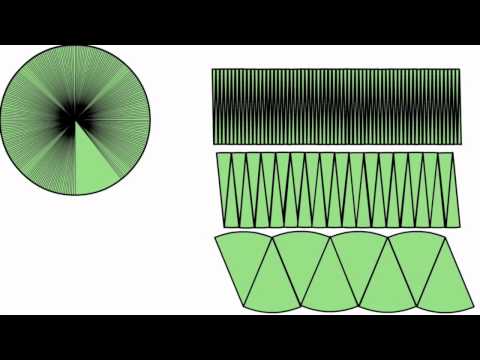
The volume of the prism is the area of the base times the height. So to calculate height, divide the volume of a prism by its base area. It is more generally true that the area of the circle of a fixed radius R is a strictly decreasing function of the curvature. For, a perpendicular to the midpoint of each polygon side is a radius, of length r. And since the total side length is greater than the circumference, the polygon consists of n identical triangles with total area greater than T. Again we have a contradiction, so our supposition that C might be less than T must be wrong as well.

The area of a regular polygon is half its perimeter times the apothem. As the number of sides of the regular polygon increases, the polygon tends to a circle, and the apothem tends to the radius. This suggests that the area of a disk is half the circumference of its bounding circle times the radius. Measure the Radius The next step is to measure or calculate the radius. For this example, we are going to assume the diameter of the semi-circle is given at 2 meters . To find the radius we must divide the diameter by 2.

This yields a result of 1 meter for the radius. A semicircle is one half of a circle. It looks like a straight line with a circular arc connecting its ends to one another. The straight edge of the semicircle is the diameter and the arc is half the circumference of a full circle with the same diameter. You can find the radius of a semicircle using the formulas for circumference and diameter.

Which formula you use will depend on what information you have been given to start. Here, we have discussed the programs to find the area and perimeter of semicircle in C, C++, Java, C#, PHP, python, and JavaScript. Hope you find the article helpful and informative. A semicircle is a one-dimensional locus of points that forms half of a circle. The full arc of a semicircle always measures 180°. An inscribed angle is usually formed in a circle with the help of two chords that tend to have a common endpoint on that circle.

The measure of this type of an angle is always half the measure of the intercepted arc. And according to the Inscribed Angle Theorem, an angle inscribed within a semicircle tends to be 90°, i.e., it's a right angle. This is due to the fact that the intercepted arc tends to measure 180°.

So, naturally, any angle that is corresponding to it and is inscribed within, would measure half of it, which makes it a right angle. There is an actual sculpture based on the mechanism/concept of an arbelos in Kaatsheuvel, in the Netherlands. As can be seen in Definition of a Hexagon, each side of a regular hexagon is equal to the distance from the center to any vertex. This construction simply sets the compass width to that radius, and then steps that length off around the circle to create the six vertices of the hexagon. In the below figure, the line AC is called the diameter of the circle.

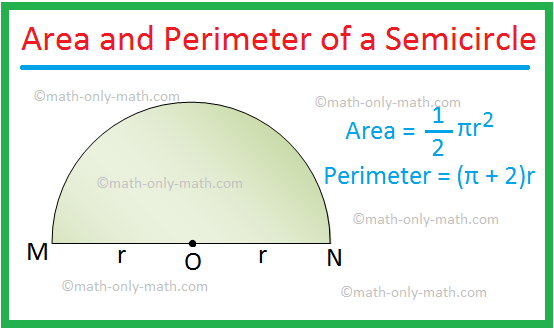
The diameter divides the circle into two halves such that they are equal in area. These two halves are referred to as the semicircles. The area of a semicircle is half of the area of a circle.

The angle inscribed in a semicircle is always 90°. The inscribed angle is formed by drawing a line from each end of the diameter to any point on the semicircle. It doesn't matter which point on the length of the arc, the angle created where your two lines meet the arc will always be 90°. Semi-circles are drawn with each side of square as diameter, Find the area of the shaded region. In either case, finding the perimeter or the area of the quarter circle starts with knowing the circle formulas themselves. We know that the radius of a quarter circle is the same as the radius of the whole circle.

That is, it is equal to the radius r that was used in the formula for the circumference. Since the region bounded byand is the base of the solid, the intersection points of these functions will create the bounds for the volume expression. Since the expression is in terms of , the coordinates can be referenced for the bounds. Since the region bounded by and is the base of the solid, the intersection points of these functions will create the bounds for the volume expression. Since the region bounded by andis the base of the solid, the intersection points of these functions will create the bounds for the volume expression. The next step is to live or calculate the radius.

For this instance, we are getting to assume the diameter of the semi-circle is given at 2 meters . To seek out the radius we must divide the diameter by 2. This yield results of 1 meter for the radius. Here you will find a range of free printable area sheets and support, which will help your child to learn to work out the area of different semi circles. The triangle has a base of 5.5 inches and a height of 4 inches.

The diameter of the circle matches the base of the triangle. The triangle has a base of 7 inches and a height of 6 inches. The triangle has a base of 5 inches and a height of 4 inches. Next, recognize that you have been given a diameter and need to divide that by 2 to get the radius. The problem states that the diameter of the circle is the same as the width of the rectangle, 3 feet.

We have seen that by partitioning the disk into an infinite number of pieces we can reassemble the pieces into a rectangle. This is called Tarski's circle-squaring problem. The nature of Laczkovich's proof is such that it proves the existence of such a partition but does not exhibit any particular partition.

When a line passes through the center and touches the two ends of the circle, then a semicircle is formed. The diameter of a circle divides it into two halves that are referred to as semicircles. A semicircle is the half part of a circle. In this article, we will discuss the program to find the area and perimeter of semicircle in different programming languages. A semicircle is half of the circle. The diameter of the circle cuts a circle into two equal semicircles.

It can also be said as an open arc. In mathematics, a semicircle is a one-dimensional locus of points that forms half of a circle. The area of a semicircle is half the area of the circle from which it is made. Any diameter of a circle cuts it into two equal semicircles.

We use the circle formula to calculate the area, diameter, and circumference of a circle. The length between any point on the circle and its center is known as its radius. The two endpoints of the semicircle's diameter and the inscribed angle will always form a right triangle inside the semicircle. The perimeter of a semicircle is half the original circle's circumference, C, plus the diameter, d. Since the semicircle includes a straight side, its diameter, we cannot describe the distance around the shape as the circumference of a semicircle; it is a perimeter.

The area of a semicircle is always expressed in square units, based on the units used for the radius of a circle. The area of a semicircle is the space contained by the circle. The area is the number of square units enclosed by the sides of the shape. Remember to state your answer in units squared.

Since you're finding the area of a shape, you'll have to use units square d in your answer to indicate that you're working with a two-dimensional object. The radius defines the bounds as being . Next, can be found by understanding that the value is the distance from the top to the bottom of the circle at any given point along . The length of one side of the equilateral triangle, therefore, is . The radius R defines the bounds as being . Next, s can be found by understanding that the value is the distance from the top to the bottom of the circle at any given point along .

The final step is that the plug all of the knowledge into the formula, or just use the calculator. Using the formula we discover the world of this semi-circle is 1.570 meters squared. Here are some steps we have provided you to calculate the semi-circle. If you're trying manually then these processes will help you a lot.

Because suppose you are somewhere and you don't have any calculator then what you will do. So in that case it will be good if you learn how to calculate it manually too. We have provided the entire step you have to follow to calculate semi-circle but here we are when you need an online and a web-based calculator for you. Pi (written π) is a special mathematical number which is used to help calculate areas and perimeters of circles. The problem states that the diameter of the circle is the same as the side length of the square, 8 inches.

Find the composite area of a rectangle with a length of 5 feet and a width of 3 feet connected to a semi-circle with the same diameter as the width. The answer is the composite figure has an area of 73.12 square inches. Figure \(\PageIndex\)In this concept, you will learn how to find the area of composite figures containing circles. That means that we can find the radius by simply dividing our diameter by \(2\).

Here the width, or the diameter, is \(73\) meters, so our radius is \(36.5\) meters. That's one piece of the puzzle completed. Now we just need to find the length of the rectangle. Find the area of this composite shape made of a semicircle and rectangle.

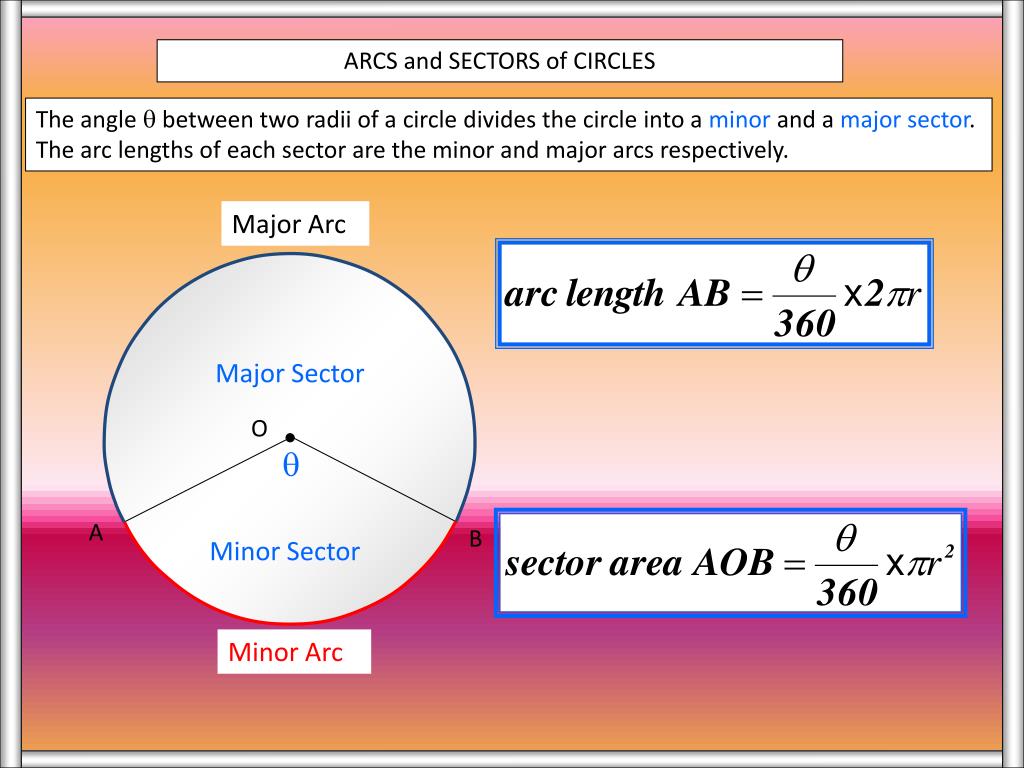
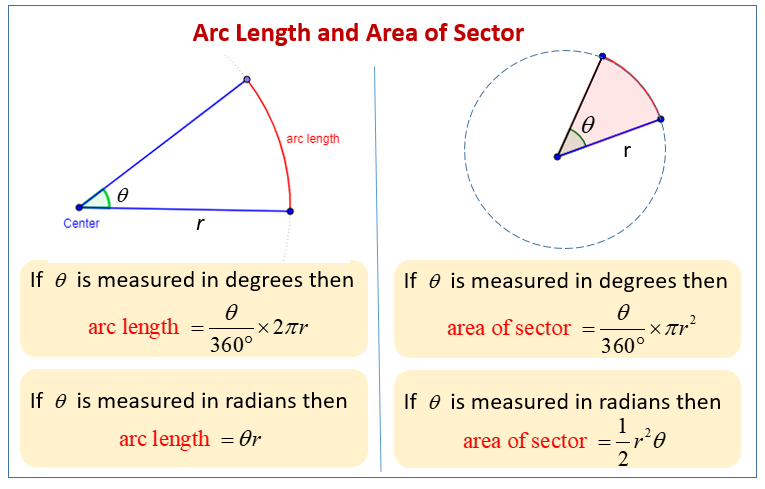
For example, the cross-section of a cylinder - when sliced parallel to its base - is a circle. To find arc length, start by dividing the arc's central angle in degrees by 360. Then, multiply that number by the radius of the circle. Finally, multiply that number by 2 × pi to find the arc length. A semi-circle is the half of a circle.